Stargate from the original article
Imagine a world where distance is no barrier, where information can travel instantaneously across vast stretches of space. This might sound like science fiction, ripped from the pages of a “Quantum Travel Superpower Wiki,” but the reality of quantum teleportation is rapidly moving from the realm of theoretical physics into practical application. While not quite the “FTL Stargate” of science fiction, quantum teleportation is a genuine quantum superpower, a groundbreaking phenomenon with the potential to revolutionize communication and computation. This exploration delves into the fascinating world of quantum teleportation, clarifying common misconceptions and illuminating the cutting-edge experiments that are pushing the boundaries of what’s possible. Inspired by the complexities and profound questions that arise from quantum teleportation, we embark on a journey to understand its intricacies and its potential to unlock unimaginable possibilities.
The path to understanding quantum teleportation is not always straightforward. Like navigating a dense quantum rabbit hole, explaining its nuances can be challenging. The subtle aspects of teleportation, particularly its seemingly instantaneous nature, often lead to misconceptions. Does quantum teleportation truly allow for superluminal transfer of information? The short answer is complex, hinting at a “probably” but stopping short of a definitive “yes.” Delving deeper requires grappling with fundamental concepts like locality and realism, concepts debated by Einstein, Podolsky, and Rosen in their seminal 1935 paper, and later challenged by Bell’s theorem in 1964. While these deeper theoretical dives are fascinating and may be explored in future discussions, for now, let’s focus on the tangible progress: the experimental verification and practical applications of quantum teleportation that are bringing this “quantum travel superpower” closer to reality.
To grasp the power of quantum teleportation, we must first revisit the foundational concepts of quantum information: qubits and entanglement. As discussed in previous explorations of building a teleportation machine, qubits, unlike classical bits, exist in a superposition of states, simultaneously representing both 0 and 1. This fundamental difference is key to the potential quantum advantage over classical computation. Using the bra-ket notation, a qubit can be represented as . This superposition principle allows quantum computers to explore multiple possibilities in parallel, offering computational power far beyond the reach of classical systems.
Entanglement, another cornerstone of quantum mechanics, introduces correlations between qubits that defy classical intuition. A “maximally entangled pair” like demonstrates this powerfully. In such a state, measuring the state of one qubit instantaneously reveals the state of the other, regardless of the distance separating them. This interconnectedness, even across space-like separations, is a crucial resource for quantum teleportation. Entangled photon pairs, for example, can be generated using spontaneous parametric down-conversion in nonlinear crystals, creating photons whose polarizations are intrinsically linked. This phenomenon, once confined to theoretical musings, is now harnessed in laboratories worldwide to create and manipulate entanglement, paving the way for practical quantum technologies.
Quantum teleportation itself, a relatively recent breakthrough in physics, emerged from theoretical proposals in 1993 by a team of researchers and was first experimentally demonstrated in 1997. Since then, continuous advancements in experimental techniques have led to remarkable achievements, most notably the experiments conducted at Qinghai Lake in Western China and in the Canary Islands. These experiments, pushing the boundaries of distance and fidelity, showcase the rapid progress in realizing quantum teleportation as a viable technology. Before diving into the details of these experiments, it’s crucial to clarify what quantum teleportation is not and what it is.
Quantum teleportation is not the Star Trek-style dematerialization and rematerialization of matter. It does not transport physical objects or living beings across distances. It is also not a method for faster-than-light communication in the sense of sending classical information instantaneously, which would violate fundamental principles of physics. Instead, quantum teleportation is a protocol for transferring the quantum state of a qubit from one location to another, using entanglement and classical communication. This seemingly subtle distinction is profound. It means that the information encoded in a qubit – its superposition state – can be perfectly reconstructed at a distant location without physically moving the qubit itself. This ability to transfer quantum information is the true “superpower” of quantum teleportation, with implications for secure communication, distributed quantum computing, and fundamental tests of quantum mechanics.
Where We Stand Experimentally:
Map of the Chinese quantum teleportation experiment setup.
Stargate from the original article
- Quantum Teleportation Across 97km in Qinghai Lake, China: Groundbreaking experiments at Qinghai Lake in Western China achieved quantum teleportation in open air over a distance of 97 kilometers. Researchers established two laboratories separated by this vast distance and generated entangled photon pairs in Alice’s lab. One photon from each pair was then transmitted to Bob’s lab, 97km away. This achievement wasn’t reliant on revolutionary new technologies, but rather on the sophisticated and meticulous integration of existing tools. Utilizing a combination of lasers at various wavelengths and classical optics components like beamsplitters and mirrors, the team overcame the challenges of long-distance quantum communication. Crucially, by opting for open-air transmission instead of fiber optics, they minimized photon loss and decoherence, which are significant hurdles in fiber-based quantum communication. This precise control and innovative application of existing technologies allowed them to establish a new distance record for quantum teleportation, demonstrating the feasibility of long-range quantum communication in real-world environments.
The Qinghai Lake team further expanded their experimental scope to include entanglement distribution. Building upon the teleportation experiment, they tackled the more complex task of generating entangled pairs at a central, third location and then distributing one photon from each pair to Alice and Bob’s separate labs. This configuration not only demonstrated entanglement distribution over long distances but also enabled them to conduct experiments aimed at “closing the locality loophole,” a crucial aspect of testing Bell’s theorem. In these experiments, the time for light to travel between Alice and Bob’s labs (300 microseconds) was significantly longer than the time it took for them to perform measurements (3 microseconds). This time separation ensured that Alice and Bob’s measurements were space-like separated, meaning no classical signal could have traveled between them during the measurement process. The results provided further experimental evidence against local realism, reinforcing the non-classical nature of quantum entanglement and its conformity with Bell’s theorem, deepening our understanding of the fundamental principles underlying quantum mechanics.
Map of the Canary Islands quantum teleportation experiment setup.
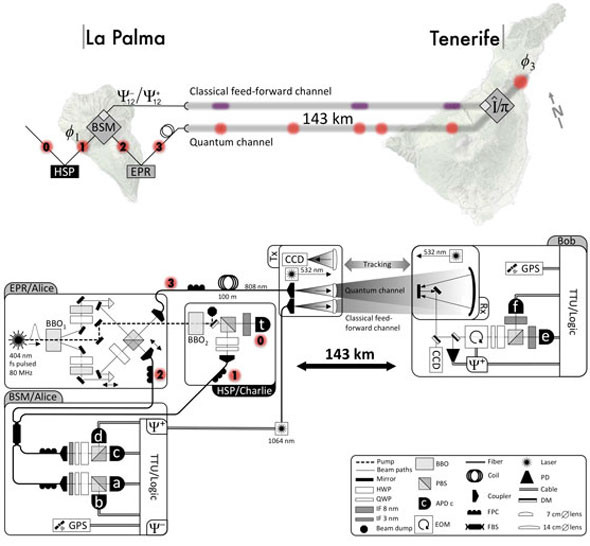Map and schematic of the Canary Islands quantum teleportation experiment (source: arXiv paper.)
- Record-Breaking 143km Teleportation in the Canary Islands: Building on the progress at Qinghai Lake, another team of researchers achieved a new distance milestone in the Canary Islands, successfully teleporting qubits 143 kilometers between the islands of La Palma and Tenerife. The Canary Islands experiment distinguished itself from the Qinghai Lake approach primarily through the implementation of an “active feed-forward technique.” While the precise details of this technique are complex, it essentially involves altering the sequence of steps in the teleportation protocol. It appears the Canary Islands team performed Step 3 (Alice’s measurement) before Step 2 (entanglement distribution in the timeline of the protocol steps). By measuring her qubits first, Alice could then send both her measurement results (classical information) and the entangled qubit (quantum channel) to Bob simultaneously. This allowed Bob to utilize the classical information in real-time, as the qubit arrived, to determine and apply the necessary quantum logic gate to his qubit, effectively reconstructing the original unknown quantum state. This active feed-forward approach, combined with other advanced techniques, allowed for more efficient and reliable teleportation over extended distances.
The Canary Islands experiment also incorporated a combination of sophisticated techniques, including a “frequency-uncorrelated polarization-entangled photon pair source,” “ultra-low-noise single-photon detectors,” and “entanglement-assisted clock synchronization.” These advanced tools, working in concert, enabled the team to perform quantum teleportation with high fidelity and reliability over the 143km open-air link. The success of both the Qinghai Lake and Canary Islands experiments is particularly exciting because these distances are comparable to those required for quantum communication with satellites in low Earth orbit (LEO). Both research teams explicitly mentioned satellite-based quantum communication as a future direction, suggesting that we may soon witness quantum teleportation between ground-based labs and LEO satellites. This rapid advancement, especially considering the relatively recent discovery of quantum teleportation just over two decades ago, underscores the remarkable progress and immense potential of this field.
For those seeking a deeper understanding, the following section breaks down the quantum teleportation protocol into a step-by-step guide:
The Quantum Teleportation Protocol: Step-by-Step
Step 0: Setting the Stage. Imagine two physicists, Alice and Bob, situated in distant laboratories, ready to perform quantum teleportation. Alice possesses an unknown qubit, represented as , which she wants to teleport to Bob. The “unknown” nature of this qubit is crucial; if Alice knew its state, simpler methods could be used for information transfer.
Step 1: Generating a Maximally Entangled Pair. Alice and Bob employ their preferred method to create a maximally entangled pair of qubits, represented as . This entangled pair serves as the quantum resource for teleportation.
Step 2: Distributing the Entangled Pair. After generation, the entangled pair needs to be distributed, with Alice and Bob each receiving one qubit. In the Qinghai Lake experiment, this was achieved by generating the pair in Alice’s lab and transmitting one photon to Bob using lasers. Now, with Alice and Bob each holding a qubit from the entangled pair, we can denote the entangled state as , where subscripts A and B indicate Alice’s and Bob’s qubits, respectively.
Step 3: Alice’s Basis Change. Alice’s objective is to transmit the unknown qubit to Bob. To teleport , we consider the combined state of the three-qubit system: Alice’s unknown qubit and the entangled pair. This joint state is described as: , which expands to . While the notation might appear complex, it simply represents the combined quantum state of the three qubits.
The key to affecting Bob’s qubit lies in Alice performing a measurement on her two qubits in the Bell basis. This measurement collapses the state of Alice’s qubits and, crucially, influences Bob’s qubit due to entanglement. Instead of measuring in the standard computational basis, Alice switches to the Bell basis. Measurement bases are a fundamental concept in quantum information, and while a detailed explanation is beyond the scope here, resources like John Preskill’s lecture notes offer comprehensive coverage. The Bell basis consists of four states:
The computational basis states can be expressed in terms of the Bell basis:
Substituting these expressions into the joint state and rearranging terms, we get:
Collecting like terms simplifies this to:
This equation shows that when Alice measures in the Bell basis, the combined state is projected into one of four possibilities, each correlated with a specific transformation of Bob’s qubit. If Alice measures her qubits and obtains, for example, , Bob’s qubit will collapse to the state .
Step 4: Alice’s Measurement. As the equations above illustrate, when Alice measures her two qubits in the Bell basis, she has an equal probability (1/4) of obtaining any of the four Bell states: , , , or . Crucially, Alice’s measurement outcome directly affects the state of Bob’s qubit. Depending on Alice’s result, Bob’s qubit will be in one of the following states: , , , or , each bearing a close resemblance to the original qubit Alice intended to teleport.
Step 5: Classical Communication. Bob now possesses a qubit that is closely related to Alice’s original qubit, but he doesn’t know which of the four possible states it is in. To complete the teleportation, Alice needs to communicate her measurement outcome to Bob using classical communication channels. Alice sends two classical bits to Bob, indicating whether she measured (represented as 00), (01), (10), or (11). This classical communication step is limited by the speed of light, which is why quantum teleportation does not enable faster-than-light communication. It is the transfer of quantum information, not classical information, that is achieved through teleportation.
Step 6: Bob’s Quantum Operation. Armed with Alice’s classical message, Bob can now transform his qubit into the exact state . This correction is achieved using quantum logic gates, analogous to classical logic gates but operating on qubits. Specifically, Bob uses the X and Z gates. The Z gate flips the sign of the coefficient of the state: . The X gate swaps the coefficients of the and states: .
Based on Alice’s measurement outcome, Bob applies the following corrections:
- If Alice sent 00 (), Bob does nothing (identity operation).
- If Alice sent 11 (), Bob applies a Z gate.
- If Alice sent 01 (), Bob applies an X gate.
- If Alice sent 10 (), Bob applies an X gate followed by a Z gate.
After applying the appropriate gate, Bob’s qubit is transformed into the precise state , successfully teleported from Alice.
Cookie brownie superposition from original article
Step 7: Bob Possesses Alice’s Qubit. Bob now holds a qubit in the state . This is not just a similar state, but an exact replica of the original unknown qubit Alice wanted to transmit. The quantum state has been teleported. It exists in superposition, and is identical to the qubit Alice started with. The quantum travel superpower is realized!
Share this:
Like Loading…
